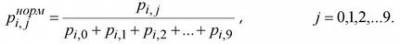| Главная » Статьи » Матпрактикум |
КИБЕРНЕТИЧЕСКАЯ МОДЕЛЬ«УЧИТЕЛЬ-УЧЕНИК»Майер Р.В. Как сказал У.Р. Эшби, кибернетика - «наука о том, как надо управлять очень сложной системой, чтобы в итоге она вела себя желательным для нас образом». Основная задача кибернетической педагогики состоит в выявлении принципов и способов эффективного управления учебным процессом, при котором минимальные затраты времени (усилий, денег) позволяют достичь требуемого уровня знаний учащихся. Решение этой проблемы требует построения абстрактной кибернетической системы учебного процесса, состоящей из множества взаимосвязанных объектов , участвующих в информационном обмене. Создание такой качественной модели позволяет осуществить математическое моделирование, а затем перейти к имитационной модели на ЭВМ.
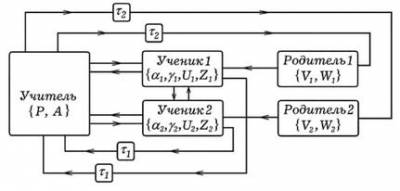
Кибернетическая система учебного процесса Построим кибернетическую систему учебного процесса. Она должна включать в себя абстрактные модели учителя, учеников и их родителей, способных воспринимать, запоминать, перерабатывать и обмениваться информацией. С целью упрощения рассуждений можно абстрагироваться от стохастического характера поведения перечисленных выше объектов и считать их детерминированными автоматами с большим числом внутренних состояний. Итак, учитель в простейшем случае моделируется автоматом, задаваемым двойкой < P , А >, где P - программа курса, А - алгоритм работы. Программа курса характеризуется списком из N вопросов (тем), их сложностью Sj и временем их изучения tj . Модель ученика задается четверкой < ОС , у , >, где ОС - коэффициент научения, у - коэффициент забывания ученика, U - уровень его притязаний из интервала [0; 1], пропорциональный оценке, на которую учащийся претендует, Z = \Z^Z2>--->Zm) ~ Знания ученика. Будем считать, что Zj - уровень знаний /'—ой темы, который лежит в интервале [0; 1] и равен вероятности правильного выполнения теста по данной теме. Модель родителя - воображаемый автомат, задаваемый двойкой < V , W >, где W - уровень притязаний родителя, V - возможность родителя оказать психологическое воздействие на своего ребенка и повысить его мотивацию к обучению U . В процессе обучения учитель воздействует на учеников, сообщая им учебную информацию и осуществляя текущий контроль (вопросы, тестирование). Учащиеся также воздействуют на учителя, сообщая, что им понятно или непонятно, задавая вопросы и выполняя задания текущего теста. Так возникает первый замкнутый контур управления. Учитель, видя реакцию учеников, может очень быстро (в течение урока) на нее реагировать: отвечать на вопросы, обращать внимание учащихся на их ошибки, помогать им их исправлять. В конце изучения темы учитель проводит контрольную работу, результаты которой также позволяют оценить уровень знаний учащихся и выбрать дальнейшую стратегию обучения: либо приступить к изучению новой темы, либо повторить изучение тех вопросов, которые были усвоены недостаточно хорошо. Это второй замкнутый контур управления. Он содержит элемент задержки, который задерживает сигнал от учащегося на время t1 (несколько дней). Рис. 1. Учебный процесс как кибернетическая система. В случае, когда учитель видит, что учащийся плохо работает, он сообщает об этом родителям. Если успехи ребенка не устраивают родителя (Z<W), и тот имеет возможность воздействовать на ребенка (V достаточно велико), то он повышает мотивацию учащегося к обучению, увеличивая его параметр U. Это третий замкнутый контур управления. Он также содержит элемент задержки на время t2 (1-2 недели). Можно усложнить систему, введя в нее новые элементы, например, директора школы, который контролирует работу учителя и результаты обучения, сопоставляя их с требуемым уровнем. При этом получится четвертый замкнутый контур управления (на рис. 1 он не изображен). Надо понимать, что в ряде случаев кибернетическая система управления претерпевает изменения. Например, в роли учителя может выступать компьютер с обучающей программой или подключенный через Интернет к какому-нибудь образовательному ресурсу. Роль родителей, повышающих мотивацию учащегося, может играть учитель, который проводит с ними воспитательную беседу, убеждает в необходимости более ответственного отношения к учебе и т.д. Компьютерная модель процесса обучения Допустим, обучаемый должен механически запомнить последовательность выполнения каких-либо действий, например, научиться считать от 0 до 9 на русском или иностранном языке, выучить алфавит, последовательность каких-то не связанных друг с другом слов, чисел и т.д. В принципе под эту ситуацию может попасть и случай, когда запоминание не механическое, элементы усваиваемой информации (операции, действия) как-то связаны между собой, но степенью связи мы пренебрегаем, либо считаем, что в среднем она несколько повышает коэффициент усвоения информации, не изменяя характера этого процесса. Пусть учащийся пытается усвоить выполнения определенной последовательности операций Oq —> Cq —> О^ —^ ... —^ Од , приводящей к решению некоторой учебной задачи. При этом процесс обучения состоит из двух этапов. На первом этапе обучаемый 5-10 раз выполняет последовательность операций Oq—> 0\—> О^—> ... —> Од вместе с учителем (компьютером, учебником), например, вслух читает алфавит . Каждый раз, когда учащийся совершает правильный переход от операции Oj к Oj+i , он учится с коэффициентом научения СС^ • Это будем учитывать так: сначала вероятность правильного перехода Pj j+\ увеличим на 0С\{\ — Pj j+\), после чего осуществим нормирование: вероятности всех переходов Pj ,• пересчитаем таким образом, чтобы их сумма была точно равна 1. Для нахождения нормированных вероятностей используется формула:
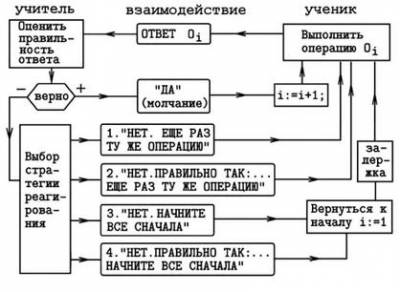
На втором этапе обучения реализуется метод проб и ошибок. Ученик по памяти пытается воспроизвести запоминаемую последовательность операций, а учитель как-то реагирует на ответы учащегося: поощряет правильные, "наказывает" или исправляет неверные действия и т.д. На рис. 2 представлен алгоритм функционирования системы "учитель - учащийся". В случае правильного ответа учащегося учитель поощряет его (говорит "Да" или молчит), при этом школьник обучается с коэффициентом научения @2 . В случае ошибочного действия Oj -^ Ок, k^i + l учитель выбирает одну из следующих четырех стратегий реагирования. Стратегия 1: "Неверно, повторите еще раз ту же операцию". При этом он "наказывает" учащегося с коэффициентом научения Q,^ . Это значит, что вероятности неправильного перехода Pjfc уменьшается на @3Pik ' а Затем осуществляется нормирование всех вероятностей Pj, (J: = 1,2,.., TV) . После этого учащийся снова пытается выбрать правильную операцию Oj+1 Рис. 2. Взаимодействие между учителем и учащимся. Стратегия 2: "Неверно. Правильно так: Oj+i . Повторите еще раз ту же операцию". При этом увеличивается вероятность правильного перехода Pf f+\ на @з0^~ Pi i+l) и ноР~ мируются остальные вероятности Pj, (J: = 1,2,..,9) . Учащийся продолжает решение задачи с операции Oj . Стратегия 3: "Неверно. Повторите всю последовательность действий с начала (с операции Cq)". Учащегося наказывают с коэффициентом обучения Q^ . При этом вероятности неправильного перехода Pfc уменьшается на Cl^Pik r после чего осуществляется нормирование всех вероятностей Pj, (J: = 0,1,..,9). Затем учащийся начинает решать задачу с самого начала. Стратегия 4: "Неверно. Правильно так: Oj-\-\ • Повторите всю последовательность действий с начала (с операции C/j)". При этом увеличивается вероятность правильного перехода Pi i+l на ^3\\~ Pi i+l) и нормируются остальные вероятности Pjj ( у = 0,1,..,9 ) . Учащийся возвращается к началу задачи. Важным вопросом является проблема оценки уровня научения учащегося. В качестве показателей успешности обучения выбраны: 1) уровень знаний (или сформированности навыка), равный среднему арифметическому вероятностей всех правильных переходов Рср =(Р01+ Р12+ Р23 +■■■ + PS9)/9 • 2) вероятность правильного выполнения всей совокупности операций (решения задачи), равная произведению вероятностей правильных переходов Рзад = P0lPnP23P34-PS9 • Компьютерная программа ПР-1 , моделирующая анализируемую ситуацию, приведена в приложении. Результаты моделирования представлены в таблице 1 и на рис. 3. В нашем случае всего было 10 операций Oj , им соответствовало 9 правильных переходов : Oq —> 0\ —> 02 —> - —> Од . Было Задано ОС\ = ОД 0С2 — &3 = ^; Число повторов в предварительном обучении равно ftj — 5. Каждый раз, когда учитель показывает правильную последовательность операций, вероятности правильных переходов при этом возрастают. После предварительного обучения (1 этап) уровень знаний был рСр = 0,47 , а вероятность правильного решения задачи Рзад =0,001. После этого моделировалось обучение методом проб и ошибок (2 этап). Решать задачу учащийся начинает с операции Oq , счетчик операций N_o увеличивается на 1. ПЭВМ выбирает случайное число X из интервала [ 0; 1 ] и методом выбора по жребию разыгрывается следующий номер операции, выбираемой учеником. Если ученик совершает правильный переход, то есть Oj—Oj_^=\ (после С/4 выбрана 0$) , то учитель хвалит учащегося, подтверждая правильность выбора. При этом вероятность правильно совершенного перехода увеличивается на Ар = (22(1 — /?[#[i' — 1]5#[/]]) г а затем нормируются вероятности Рц (у = 0,1,..,9) так, чтобы их сумма была равна 1. Если ученик совершил неправильный переход (Oj — Oj_^ ФI) , то учитель наказывает ученика. Если при этом он не подсказывает правильный выбор, то вероятность неверно совершенного перехода уменьшается на Ар = Q^p\o\i' — 1],о[/]], после чего вероятности Pjj нормируются. В случае, когда учитель подсказывает правильный ответ, то используется другой алгоритм: вероятность неверно совершенного перехода уменьшается на Ар , а вероятность правильного перехода от Oj_i к Oj_i +I увеличивается на Ар . Сумма вероятностей всех переходов остается равной 1. Используется метод статистических испытаний. Программа делает 200 циклов (испытаний) и каждый раз вычисляет общее число ответов Tvj, число ошибочных ответов Л^2 / общее время обучения t = (N1 - N2)Ati + N2At2 , которое не должно превзойти заданное значение ^max = о00 условных единиц времени. Когда это происходит, программа выходит из цикла, заканчивается данное испытание, результаты выводятся на экран ПЭВМ. В нашем случае At^ =1 (усл. ед. вр.), А/о =2 усл. ед. вр., то есть на ошибочный ответ и его исправление затрачивается в 2 раза больше времени, чем на правильный ответ. Таблица 1. Из таблицы 1 видно, что при заданных параметрах модели наиболее эффективной является стратегия 2 ("Нет. Правильно так. Повторите еще раз ту же операцию") и стратегия 4 ("Нет. Правильно так. Повторите все с начала"). Эти стратегии поведения учителя предполагают подсказку учащимся правильного выбора операции. При использовании учителем стратегии 4 учащийся дает максимальное количество ответов при минимальном числе ошибок. Стратегия 1 ("Нет. Повторите еще раз ту же операцию") является самой неэффективной. Стратегии 3 и 4, предусматривающие возврат учащегося к началу выполнения всех действий, приводят к тому, что он чаще выполняет первые операции 0\, 0*2 , Оу , 0\ и реже последние Og , Oj , Og , Og . Поэтому после второго этапа обучения вероятности переходов Pq\ , Р\2 / Pj2> ' РЪА' достаточно высоки, в то время как вероятности /?5g, /?67 ' PlS' PS9 малы/ что приводит к низкой вероятности Рзад решения всей задачи. Стратегии 1 и 2 не требуют возврата учащегося к началу задачи, - после ошибки он продолжает выполнять действия с того места, где он совершил ошибку. Поэтому вероятности правильных переходов после второго этапа обучения примерно одинаковы. Стратегия 2 эффективнее стратегии 1 потому, что при ее использовании учитель подсказывает правильный выбор операции.
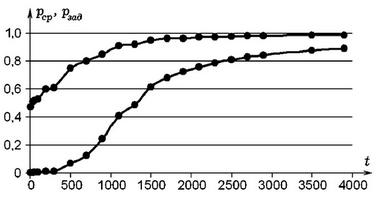
Рис. 3. Типичная зависимость Реп и Рзад от времени обучения. Для изучения зависимости уровня знаний Реп и вероятности Р^ад решения задачи от времени обучения методом проб и ошибок был проведен вычислительный эксперимент, в котором задавалось время обучения t и определялись средние значения РСг> и Р зад кажДыи Ра3 Лля ЮО испытаний. При этом использовалась стратегия 1. Получающиеся графики представлены на рис. 3. Видно, что в процессе обучения кривая научения растет по логистическому закону от 0,47 (уровень после предварительного обучения) до 1. Вероятность правильного выполнения задачи Рзад сначала невелика, затем также возрастает, стремясь к 1. При использовании других стратегий характер изменения рСг> и Рзад такои же, скорость возрастания больше. Приложение Программа ПР-1 uses crt; {Free Pascal} const N=10; K_is=100; al=0.1; a2=0.2; a3=0.2; slovo:array[1..10]of integer=(0,1,2,3,4,5,6,7,8,9); var kol_isp,time,N_o,N_pr,N_osh,k,l,i,il,i2,j: integer; p: array[0..N,0..N] of real; o: array [-l..N]of integer; N1,N2,Z1,Z2,P_sr,P_zad,dp,x,sum_p,sum,tt : real; Label mm; Procedure Pechat; begin {raspechatka massiva p} For il:=0 to 9 do begin writeln; For i2:=0 to 9 do write(' ',p[il,i2]:2:3); end; writeln; end; Procedure Normir; {normirovanie p} begin sum:=0; For j:=0 to N-l do sum:=sum+p[o[i-1],j]; For j:=0 to N-l do p[o[i-1],j]:=p[o[i-1],j]/sum; end; BEGIN clrscr; Repeat k:=0; For i:=0 to N do For j:=0 to N do p[i,j]:=l/N; Repeat inc(k); randomize; i2:=0; {1. PREDVARITELNOE OBUCHENIE} For i:=2 to 10 do begin il:=slovo[i]; p[i2,il]:=p[i2,il]+al*(l-p[i2,il]); For j:=0 to N-l do begin If jOil then p[i2, j] :=p[i2, j ]-al* (1-p [i2 ,il] ) / (N-l) ; end; i2:=il; end; until (k=5)or(Keypressed); {Pechat;} {2. OBUCHENIE METODOM PROB I OSHIBOK} 1:=0; N_osh:=0; N_o:=0; Repeat inc(l); o[0]:=0; For i:=0 to 8 do begin inc(N_o); sum_p:=0; x:=random(100)/100; for j:=0 to N-l do begin sum_p:=sum_p+p[i,j]; If x>sum_p then o[i]:=j+l; end; {uchenik vibiraet opraciu} If (o[i]-o[i-l]=l)and(i<9) then begin inc(N_pr); {verno} p[o[i-l],o[i]]:=p[o[i-l],o[i]]+a2*(1-p[o[i-1],o[i]]); Normir; end; (*If о[i]-o[i-l]<>l then begin inc(N_osh); {neverno} p[o[i-l],o[i-l]+l]:=p[o[i-l],o[i-l]+l] +a3*p[o[i-l],o[i-l]+l]; Normir; goto mm; {o[i]:=o[i-1];} end; end; mm: {2 i 4 strategii} *) If о[i]-o[i-l]<>l then begin inc(N_osh); {neverno} p[o[i-l],o[i]]:=p[o[i-l],o[i]]-a3*p[o[i-l],o[i]]; Normir; {goto mm;} о[i]:=o[i-1]; end; end; mm: {1 i 3 strategii} until (N_o+N_osh>800)or(Keypressed); {Pechat;} time:=N_o+N_osh; inc(kol_isp); P_sr:=(p[0,l]+p[l,2]+p[2,3]+p[3,4] +p[4,5]+p[5,6]+p[6,7]+p[7,8]+p[8,9])/9; P_zad:=p[0,l]*p[l,2]*p[2,3]*p[3,4]*p[4,5] *p[5,6]*p[6,7]*p[7,8]*p[8,9]; writeln(N_o,' Kol_osh ',N_osh,' Vrem ',time, ' P_sr ',P_sr,' P_zad ',P_zad); Nl:=Nl+N_o; N2:=N2+N_osh; tt:=tt+time; Zl:=Zl+P_sr; Z2:=Z2+P_zad; until (Keypressed)or(kol_isp=K_is); writeln('Kol_otv ',N1/K_is,' Kol_osh ',N2/K_is, ' Vremya ',tt/K_is); writeln(' P_sr ',Z1/K_is,' P_zad ',Z2/K_is); readkey; END. Литература
| |
| Просмотров: 2233 | |
| Всего комментариев: 0 | |